STA 326 2.0 Programming and Data Analysis with RLesson 5.2: SimulationsDr Thiyanga Talagala2020-03-101 / 11

Monty Hall Problem

Image Credit: Ben Bennetts

2 / 11

3 / 11

4 / 11

Monty Hall Problem: RulesThe host must always open a door that was not picked by the contestant.
5 / 11

Monty Hall Problem: RulesThe host must always open a door that was not picked by the contestant.
The host must always open a door to reveal a goat and never the car.
5 / 11

Monty Hall Problem: Rules

The host must always open a door that was not picked by the contestant.

The host must always open a door to reveal a goat and never the car.

The host must always offer the chance to switch between the originally chosen door and the remaining closed door.
```
     Taken from https://en.wikipedia.org/wiki/Monty_Hall_problem
```

5 / 11

Let's play the game!

Click here to play: http://www.math.ucsd.edu/~crypto/Monty/monty.html

Does switching increases the chance of winning the car?

6 / 11

We use sample function to assign car, goat, goat, behind the doors.

sample(c("car", "goat", "goat"))

[1] "goat" "goat" "car"

sample(c("car", "goat", "goat"))

[1] "goat" "car"  "goat"

7 / 11

We use sample function to assign car, goat, goat, behind the doors.

sample(c("car", "goat", "goat"))

[1] "goat" "goat" "car"

sample(c("car", "goat", "goat"))

[1] "goat" "car"  "goat"

Here is a function that will take player's initial choice of door.

select_first_door <- function(door){
  door.allocation <- sample(c("car", "goat", "goat"))
  door.allocation[door]
}
select_first_door(2) # My first choice is the 2nd door

[1] "goat"

7 / 11

We use sample function to assign car, goat, goat, behind the doors.

sample(c("car", "goat", "goat"))

[1] "goat" "goat" "car"

sample(c("car", "goat", "goat"))

[1] "goat" "car"  "goat"

Here is a function that will take player's initial choice of door.

select_first_door <- function(door){
  door.allocation <- sample(c("car", "goat", "goat"))
  door.allocation[door]
}
select_first_door(2) # My first choice is the 2nd door

[1] "goat"

Modify your function so that it shows the player the door that the host selects. Hint: sample function act as a host.

7 / 11

Modify your function so that it includes the player strategy (switch or stay) as an input, and returns the appropriate result.

Run your function 1000 times, for each strategy and report the proportion of times that car is selected. (You could put this in a loop and compute the proportion of times car shows.)
How many times would you expect car to be selected out of 1000 runs?

8 / 11

Approximating Pi = 3.14616

$\frac{A_{c i r c l e}}{A_{s q u a r e}} = \frac{π r^{2}}{4 r^{2}}$ Equation of a circle center around 0: $x^{2} + y^{2} = r^{2}$

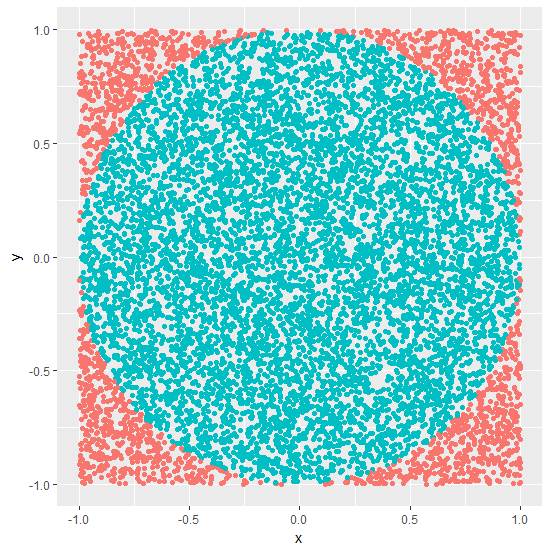
Write a function to approximate $π$ using Monte Carlo simulations.

9 / 11

Random Variable Generation: Inverse-Transform Method

Let $X$ be a random variable with CDF $F$ . Since $F$ is a nondecreasing function, the inverse function $F^{- 1}$ may be defined as $F^{- 1} (y) = i n f {x : F (x) \geq y}, 0 \leq y \leq 1.$

It is easy to show that if $U \sim U (0, 1)$ , then

$X = F^{- 1} (U)$

has CDF $F$ . Namely, since $F$ is invertible and $P (U \leq u) = u$ , we have

$P (X \leq x) = P (F^{- 1} (U) \leq x) = P (U \leq F (x)) = F (x)$

10 / 11

Slides available at: hellor.netlify.com

11 / 11

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Start & Stop the presentation timer

Reset the presentation timer

?, h

Toggle this help