class: center, middle, inverse, title-slide # STA 517 3.0 Programming and Statistical Computing with R ## An Introduction to the Bootstrap Method ### Dr Thiyanga Talagala --- <!--https://statisticsbyjim.com/hypothesis-testing/bootstrapping/--> # What is a bootstrap? - Bootstrap is a method of inference. - Bradley Efron first introduced this approach in 1979. - Link to his original paper is [here](https://projecteuclid.org/euclid.aos/1176344552).  - Bootstrapping is a computer-intensive procedure. --- # Applications - Estimate the standard error of any statistic and to obtain a confidence interval (CI) for it. - This is useful when CI doesn't have a closed form, or it has a very complicated one. - Hypothesis testing - Bootstrap sampling in regression, etc. ## Three forms of bootstrapping - Nonparametric (resampling) - Semiparametric (adding noise) - Parametric (simulation) <!--https://online.stat.psu.edu/stat555/node/119/--> <!--There are three forms of bootstrapping which differ primarily in how the population is estimated. Most people who have heard of bootstrapping have only heard of the so-called nonparametric or resampling bootstrap.--> --- ## Bootstrapping Resamples - The bootstrap sample is the same size as the original sample data. - As a result, some observations will be represented multiple times in the bootstrap sample while others will not be selected at all. 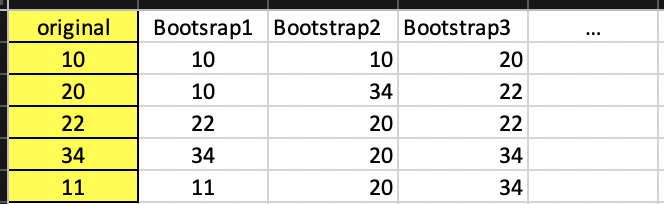## Example of Bootstrap Samples  - Bootstrapping does not take new observations from the population. - It treats the original sample as a proxy for the real population and then draws random samples from it. - Consequently, the central assumption for bootstrapping is that the original sample accurately represents the actual population. --- # Steps 1. Take a sample from population. This is called the **original sample**. Suppose the sample size is `\(n\)`. 2. Draw a sample from the original sample data with replacement with size `\(n\)` and repeat this step `\(N\)` times. 3. Compute the statistic of `\(\theta\)` for each Bootstrap Sample, and there will be totally `\(N\)` estimates of `\(\theta\)`. 4. Construct a sampling distribution with these `\(N\)` Bootstrap statistics and use it to make further statistical inference. ---  --- ## Differences between Bootstrapping and Traditional Inference Methods - how they estimate sampling distributions - "The traditional approach also uses theory to tell what the sampling distribution should look like, but the results fall apart if the assumptions of the theory are not met. The bootstrapping method, on the other hand, takes the original sample data and then resamples it to create many bootstrap samples." > source: towards data science. <!--https://towardsdatascience.com/bootstrapping-statistics-what-it-is-and-why-its-used-e2fa29577307#:~:text=The%20traditional%20approach%20also%20uses,create%20many%20%5Bsimulated%5D%20samples.--> --- ## Example 1 <!--http://bcs.whfreeman.com/webpub/statistics/ips9e/9781319013387/companionchapters/companionchapter16.pdf--> Height of randomly selected individuals ```r height <- c(5.2, 6.1, 5.5, 5.4, 5.3) height ``` ``` [1] 5.2 6.1 5.5 5.4 5.3 ``` 1. Construct 1000 bootstrap samples. 2. Calculate the sample mean for each of the resamples. 3. Make a histogram of the means of the 1000 bootstrap samples. This is the bootstrap distribution. 4. Calculate the bootstrap standard error. --- ## Example 1 (cont.) Help: `$$\bar{X*} = \frac{1}{N}\sum_{i=1}^N\bar{x}_{i}^{bootstrap}$$` `$$se(\bar{X*}) =\sqrt{\frac{1}{N-1}\sum_{i=1}^N (\bar{x}_{i}^{bootstrap} - \bar{X*})^2}$$` The bootstrap standard error, of a statistic is the standard deviation of the bootstrap distribution of that statistic. --- ## Classical confidence interval `$$[\bar{x}- t_{\alpha/2, n-1}se(\bar{x}), \bar{x}- t_{\alpha/2, n-1}se(\bar{x})]$$` ## Confidence intervals via bootstrap - `boot` package can generate bootstrap samples. - Step 1: To use the `boot` function for drawing samples, you need a function to compute the statistic of interest. ```r samplemean <- function(data, indices) { return(mean(data[indices])) } ``` It should have at least two arguments: i) `data`: the original data ii) a vector containing `indices`: frequencies or weights which define the bootstrap sample. `data[indices]` Creates the bootstrap sample (i.e., subset the provided data by the “indices” parameter). “indices” is automatically provided by the “boot” function; this is the sampling with replacement portion of bootstrapping. --- ## Confidence intervals via bootstrap (cont.) Step 2: Conduct the bootstrapping ```r library(boot) result <- boot(data = height, statistic = samplemean, R = 1000) result ``` ``` ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = height, statistic = samplemean, R = 1000) Bootstrap Statistics : original bias std. error t1* 5.5 0.00528 0.1402647 ``` <!--http://people.tamu.edu/~alawing/materials/ESSM689/Btutorial.pdf--> --- ## View some calculated statistics of boot object .pull-left[ **Bootstrap sample means** ```r result$t ``` ``` [,1] [1,] 5.38 [2,] 5.52 [3,] 5.46 [4,] 5.50 [5,] 5.64 [6,] 5.60 [7,] 5.40 [8,] 5.66 [9,] 5.54 [10,] 5.50 [11,] 5.50 [12,] 5.70 [13,] 5.32 [14,] 5.36 [15,] 5.52 [16,] 5.60 [17,] 5.46 [18,] 5.48 [19,] 5.40 [20,] 5.54 [21,] 5.50 [22,] 5.48 [23,] 5.56 [24,] 5.38 [25,] 5.40 [26,] 5.32 [27,] 5.46 [28,] 5.60 [29,] 5.64 [30,] 5.54 [31,] 5.72 [32,] 5.32 [33,] 5.48 [34,] 5.64 [35,] 5.52 [36,] 5.32 [37,] 5.32 [38,] 5.34 [39,] 5.60 [40,] 5.36 [41,] 5.52 [42,] 5.68 [43,] 5.68 [44,] 5.32 [45,] 5.50 [46,] 5.46 [47,] 5.50 [48,] 5.48 [49,] 5.38 [50,] 5.64 [51,] 5.36 [52,] 5.54 [53,] 5.64 [54,] 5.38 [55,] 5.70 [56,] 5.66 [57,] 5.50 [58,] 5.54 [59,] 5.62 [60,] 5.50 [61,] 5.50 [62,] 5.54 [63,] 5.30 [64,] 5.62 [65,] 5.64 [66,] 5.36 [67,] 5.34 [68,] 5.36 [69,] 5.26 [70,] 5.70 [71,] 5.54 [72,] 5.54 [73,] 5.68 [74,] 5.38 [75,] 5.62 [76,] 5.78 [77,] 5.52 [78,] 5.52 [79,] 5.24 [80,] 5.54 [81,] 5.44 [82,] 5.68 [83,] 5.82 [84,] 5.78 [85,] 5.58 [86,] 5.86 [87,] 5.54 [88,] 5.46 [89,] 5.60 [90,] 5.36 [91,] 5.42 [92,] 5.58 [93,] 5.40 [94,] 5.26 [95,] 5.48 [96,] 5.58 [97,] 5.44 [98,] 5.48 [99,] 5.50 [100,] 5.50 [101,] 5.46 [102,] 5.28 [103,] 5.26 [104,] 5.28 [105,] 5.48 [106,] 5.36 [107,] 5.66 [108,] 5.62 [109,] 5.80 [110,] 5.72 [111,] 5.42 [112,] 5.36 [113,] 5.80 [114,] 5.68 [115,] 5.44 [116,] 5.56 [117,] 5.64 [118,] 5.28 [119,] 5.46 [120,] 5.28 [121,] 5.46 [122,] 5.64 [123,] 5.62 [124,] 5.50 [125,] 5.32 [126,] 5.52 [127,] 5.26 [128,] 5.66 [129,] 5.40 [130,] 5.78 [131,] 5.50 [132,] 5.30 [133,] 5.66 [134,] 5.50 [135,] 5.60 [136,] 5.26 [137,] 5.66 [138,] 5.52 [139,] 5.56 [140,] 5.48 [141,] 5.30 [142,] 5.32 [143,] 5.34 [144,] 5.56 [145,] 5.56 [146,] 5.86 [147,] 5.38 [148,] 5.40 [149,] 5.72 [150,] 5.48 [151,] 5.54 [152,] 5.58 [153,] 5.62 [154,] 5.50 [155,] 5.50 [156,] 5.52 [157,] 5.52 [158,] 5.82 [159,] 5.68 [160,] 5.50 [161,] 5.46 [162,] 5.48 [163,] 5.26 [164,] 5.56 [165,] 5.54 [166,] 5.42 [167,] 5.52 [168,] 5.44 [169,] 5.48 [170,] 5.64 [171,] 5.64 [172,] 5.58 [173,] 5.36 [174,] 5.48 [175,] 5.34 [176,] 5.38 [177,] 5.44 [178,] 5.32 [179,] 5.48 [180,] 5.58 [181,] 5.44 [182,] 5.38 [183,] 5.74 [184,] 5.32 [185,] 5.48 [186,] 5.34 [187,] 5.72 [188,] 5.56 [189,] 5.52 [190,] 5.50 [191,] 5.40 [192,] 5.60 [193,] 5.28 [194,] 5.36 [195,] 5.68 [196,] 5.64 [197,] 5.52 [198,] 5.54 [199,] 5.34 [200,] 5.28 [201,] 5.76 [202,] 5.48 [203,] 5.60 [204,] 5.52 [205,] 5.52 [206,] 5.54 [207,] 5.52 [208,] 5.56 [209,] 5.54 [210,] 5.40 [211,] 5.46 [212,] 5.84 [213,] 5.64 [214,] 5.30 [215,] 5.48 [216,] 5.54 [217,] 5.50 [218,] 5.34 [219,] 5.36 [220,] 5.38 [221,] 5.44 [222,] 5.44 [223,] 5.52 [224,] 5.26 [225,] 5.82 [226,] 5.38 [227,] 5.80 [228,] 5.32 [229,] 5.22 [230,] 5.32 [231,] 5.52 [232,] 5.30 [233,] 5.54 [234,] 5.80 [235,] 5.34 [236,] 5.62 [237,] 5.66 [238,] 5.34 [239,] 5.62 [240,] 5.66 [241,] 5.32 [242,] 5.62 [243,] 5.62 [244,] 5.52 [245,] 5.36 [246,] 5.54 [247,] 5.50 [248,] 5.50 [249,] 5.66 [250,] 5.52 [251,] 5.54 [252,] 5.44 [253,] 5.50 [254,] 5.50 [255,] 5.70 [256,] 5.72 [257,] 5.64 [258,] 5.78 [259,] 5.54 [260,] 5.42 [261,] 5.38 [262,] 5.38 [263,] 5.48 [264,] 5.50 [265,] 5.28 [266,] 5.32 [267,] 5.48 [268,] 5.48 [269,] 5.66 [270,] 5.54 [271,] 5.70 [272,] 5.80 [273,] 5.78 [274,] 5.50 [275,] 5.86 [276,] 5.42 [277,] 5.66 [278,] 5.38 [279,] 5.48 [280,] 5.66 [281,] 5.44 [282,] 5.68 [283,] 5.64 [284,] 5.66 [285,] 5.50 [286,] 5.56 [287,] 5.60 [288,] 5.58 [289,] 5.48 [290,] 5.36 [291,] 5.30 [292,] 5.54 [293,] 5.52 [294,] 5.34 [295,] 5.52 [296,] 5.54 [297,] 5.66 [298,] 5.42 [299,] 5.38 [300,] 5.44 [301,] 5.50 [302,] 5.36 [303,] 5.56 [304,] 5.52 [305,] 5.34 [306,] 5.34 [307,] 5.74 [308,] 5.64 [309,] 5.76 [310,] 5.40 [311,] 5.50 [312,] 5.40 [313,] 5.42 [314,] 5.46 [315,] 5.70 [316,] 5.52 [317,] 5.64 [318,] 5.68 [319,] 5.32 [320,] 5.40 [321,] 5.42 [322,] 5.50 [323,] 5.44 [324,] 5.50 [325,] 5.46 [326,] 5.68 [327,] 5.32 [328,] 5.30 [329,] 5.32 [330,] 5.50 [331,] 5.66 [332,] 5.66 [333,] 5.32 [334,] 5.58 [335,] 5.50 [336,] 5.32 [337,] 5.68 [338,] 5.48 [339,] 5.50 [340,] 5.50 [341,] 5.48 [342,] 5.36 [343,] 5.60 [344,] 5.34 [345,] 5.48 [346,] 5.38 [347,] 5.42 [348,] 5.80 [349,] 5.48 [350,] 5.48 [351,] 5.26 [352,] 5.54 [353,] 5.44 [354,] 5.50 [355,] 5.80 [356,] 5.26 [357,] 5.50 [358,] 5.64 [359,] 5.30 [360,] 5.48 [361,] 5.34 [362,] 5.62 [363,] 5.50 [364,] 5.82 [365,] 5.68 [366,] 5.52 [367,] 5.44 [368,] 5.78 [369,] 5.50 [370,] 5.52 [371,] 5.36 [372,] 5.68 [373,] 5.50 [374,] 5.36 [375,] 5.42 [376,] 5.38 [377,] 5.68 [378,] 5.46 [379,] 5.40 [380,] 5.80 [381,] 5.66 [382,] 5.46 [383,] 5.54 [384,] 5.56 [385,] 5.32 [386,] 5.60 [387,] 5.48 [388,] 5.40 [389,] 5.54 [390,] 5.28 [391,] 5.50 [392,] 5.34 [393,] 5.54 [394,] 5.68 [395,] 5.32 [396,] 5.36 [397,] 5.50 [398,] 5.44 [399,] 5.54 [400,] 5.42 [401,] 5.66 [402,] 5.56 [403,] 5.32 [404,] 5.82 [405,] 5.56 [406,] 5.44 [407,] 5.72 [408,] 5.62 [409,] 5.72 [410,] 5.66 [411,] 5.60 [412,] 5.52 [413,] 5.48 [414,] 5.58 [415,] 5.30 [416,] 5.46 [417,] 5.26 [418,] 5.38 [419,] 5.34 [420,] 5.56 [421,] 5.44 [422,] 5.46 [423,] 5.66 [424,] 5.62 [425,] 5.52 [426,] 5.32 [427,] 5.70 [428,] 5.66 [429,] 5.50 [430,] 5.62 [431,] 5.36 [432,] 5.64 [433,] 5.66 [434,] 5.40 [435,] 5.26 [436,] 5.58 [437,] 5.48 [438,] 5.70 [439,] 5.48 [440,] 5.74 [441,] 5.52 [442,] 5.42 [443,] 5.52 [444,] 5.64 [445,] 5.78 [446,] 5.30 [447,] 5.52 [448,] 5.38 [449,] 5.46 [450,] 5.36 [451,] 5.30 [452,] 5.34 [453,] 5.62 [454,] 5.50 [455,] 5.52 [456,] 5.66 [457,] 5.60 [458,] 5.48 [459,] 5.50 [460,] 5.66 [461,] 5.48 [462,] 5.40 [463,] 5.32 [464,] 5.52 [465,] 5.34 [466,] 5.68 [467,] 5.72 [468,] 5.60 [469,] 5.40 [470,] 5.58 [471,] 5.50 [472,] 5.46 [473,] 5.62 [474,] 5.44 [475,] 5.52 [476,] 5.54 [477,] 5.40 [478,] 5.74 [479,] 5.34 [480,] 5.46 [481,] 5.52 [482,] 5.30 [483,] 5.50 [484,] 5.60 [485,] 5.76 [486,] 5.52 [487,] 5.50 [488,] 5.70 [489,] 5.62 [490,] 5.40 [491,] 5.46 [492,] 5.48 [493,] 5.34 [494,] 5.54 [495,] 5.40 [496,] 5.38 [497,] 5.52 [498,] 5.54 [499,] 5.50 [500,] 5.42 [501,] 5.54 [502,] 5.70 [503,] 5.36 [504,] 5.34 [505,] 5.36 [506,] 5.46 [507,] 5.38 [508,] 5.34 [509,] 5.40 [510,] 5.44 [511,] 5.48 [512,] 5.74 [513,] 5.46 [514,] 5.40 [515,] 5.26 [516,] 5.44 [517,] 5.50 [518,] 5.52 [519,] 5.78 [520,] 5.50 [521,] 5.30 [522,] 5.30 [523,] 5.34 [524,] 5.42 [525,] 5.28 [526,] 5.56 [527,] 5.50 [528,] 5.66 [529,] 5.66 [530,] 5.62 [531,] 5.30 [532,] 5.62 [533,] 5.50 [534,] 5.82 [535,] 5.58 [536,] 5.66 [537,] 5.30 [538,] 5.84 [539,] 5.56 [540,] 5.40 [541,] 5.30 [542,] 5.84 [543,] 5.42 [544,] 5.24 [545,] 5.60 [546,] 5.58 [547,] 5.60 [548,] 5.56 [549,] 5.82 [550,] 5.34 [551,] 5.70 [552,] 5.64 [553,] 5.48 [554,] 5.36 [555,] 5.32 [556,] 5.48 [557,] 5.48 [558,] 5.48 [559,] 5.64 [560,] 5.48 [561,] 5.38 [562,] 5.62 [563,] 5.38 [564,] 5.52 [565,] 5.44 [566,] 5.78 [567,] 5.58 [568,] 5.66 [569,] 5.40 [570,] 5.46 [571,] 5.30 [572,] 5.48 [573,] 5.48 [574,] 5.64 [575,] 5.34 [576,] 5.48 [577,] 5.72 [578,] 5.40 [579,] 5.58 [580,] 5.48 [581,] 5.44 [582,] 5.68 [583,] 5.66 [584,] 5.64 [585,] 5.66 [586,] 5.34 [587,] 5.50 [588,] 5.38 [589,] 5.50 [590,] 5.96 [591,] 5.66 [592,] 5.54 [593,] 5.48 [594,] 5.36 [595,] 5.64 [596,] 5.42 [597,] 5.42 [598,] 5.54 [599,] 5.34 [600,] 5.48 [601,] 5.68 [602,] 5.32 [603,] 5.30 [604,] 5.42 [605,] 5.48 [606,] 5.52 [607,] 5.58 [608,] 5.36 [609,] 5.38 [610,] 5.66 [611,] 5.64 [612,] 5.46 [613,] 5.34 [614,] 5.46 [615,] 5.48 [616,] 5.56 [617,] 5.52 [618,] 5.40 [619,] 5.32 [620,] 5.38 [621,] 5.26 [622,] 5.44 [623,] 5.50 [624,] 5.76 [625,] 5.66 [626,] 5.30 [627,] 5.30 [628,] 5.38 [629,] 5.56 [630,] 5.48 [631,] 5.40 [632,] 5.30 [633,] 5.28 [634,] 5.50 [635,] 5.48 [636,] 5.40 [637,] 5.54 [638,] 5.50 [639,] 5.54 [640,] 5.68 [641,] 5.30 [642,] 5.34 [643,] 5.20 [644,] 5.80 [645,] 5.34 [646,] 5.50 [647,] 5.34 [648,] 5.50 [649,] 5.48 [650,] 5.42 [651,] 5.52 [652,] 5.62 [653,] 5.50 [654,] 5.62 [655,] 5.50 [656,] 5.74 [657,] 5.62 [658,] 5.54 [659,] 5.34 [660,] 5.32 [661,] 5.42 [662,] 5.32 [663,] 5.66 [664,] 5.60 [665,] 5.52 [666,] 5.48 [667,] 5.36 [668,] 5.64 [669,] 5.52 [670,] 5.66 [671,] 5.62 [672,] 5.42 [673,] 5.34 [674,] 5.60 [675,] 5.28 [676,] 5.46 [677,] 5.44 [678,] 5.66 [679,] 5.70 [680,] 5.54 [681,] 5.64 [682,] 5.54 [683,] 5.52 [684,] 5.78 [685,] 5.38 [686,] 5.80 [687,] 5.42 [688,] 5.38 [689,] 5.48 [690,] 5.32 [691,] 5.56 [692,] 5.28 [693,] 5.28 [694,] 5.52 [695,] 5.52 [696,] 5.46 [697,] 5.50 [698,] 5.54 [699,] 5.30 [700,] 5.50 [701,] 5.62 [702,] 5.60 [703,] 5.44 [704,] 5.44 [705,] 5.66 [706,] 5.36 [707,] 5.46 [708,] 5.36 [709,] 5.46 [710,] 5.36 [711,] 5.52 [712,] 5.52 [713,] 5.44 [714,] 5.50 [715,] 5.64 [716,] 5.40 [717,] 5.60 [718,] 5.50 [719,] 5.50 [720,] 5.32 [721,] 5.40 [722,] 5.54 [723,] 5.42 [724,] 5.30 [725,] 5.36 [726,] 5.30 [727,] 5.40 [728,] 5.48 [729,] 5.68 [730,] 5.40 [731,] 5.52 [732,] 5.50 [733,] 5.46 [734,] 5.58 [735,] 5.44 [736,] 5.52 [737,] 5.64 [738,] 5.46 [739,] 5.50 [740,] 5.62 [741,] 5.54 [742,] 5.68 [743,] 5.64 [744,] 5.52 [745,] 5.50 [746,] 5.64 [747,] 5.34 [748,] 5.80 [749,] 5.54 [750,] 5.64 [751,] 5.48 [752,] 5.52 [753,] 5.50 [754,] 5.72 [755,] 5.64 [756,] 5.52 [757,] 5.62 [758,] 5.36 [759,] 5.40 [760,] 5.50 [761,] 5.72 [762,] 5.54 [763,] 5.48 [764,] 5.64 [765,] 5.68 [766,] 5.72 [767,] 5.36 [768,] 5.46 [769,] 5.56 [770,] 5.64 [771,] 5.48 [772,] 5.60 [773,] 5.66 [774,] 5.36 [775,] 5.36 [776,] 5.54 [777,] 5.34 [778,] 5.78 [779,] 5.48 [780,] 5.64 [781,] 5.40 [782,] 5.46 [783,] 5.40 [784,] 5.44 [785,] 5.78 [786,] 5.30 [787,] 5.64 [788,] 5.24 [789,] 5.70 [790,] 5.44 [791,] 5.38 [792,] 5.38 [793,] 5.72 [794,] 5.50 [795,] 5.34 [796,] 5.64 [797,] 5.74 [798,] 5.54 [799,] 5.46 [800,] 5.48 [801,] 5.42 [802,] 5.48 [803,] 5.50 [804,] 5.40 [805,] 5.64 [806,] 5.60 [807,] 5.52 [808,] 5.42 [809,] 5.50 [810,] 5.70 [811,] 5.52 [812,] 5.50 [813,] 5.38 [814,] 5.36 [815,] 5.38 [816,] 5.62 [817,] 5.24 [818,] 5.56 [819,] 5.40 [820,] 5.44 [821,] 5.50 [822,] 5.62 [823,] 5.36 [824,] 5.56 [825,] 5.48 [826,] 5.40 [827,] 5.50 [828,] 5.48 [829,] 5.50 [830,] 5.32 [831,] 5.54 [832,] 5.58 [833,] 5.66 [834,] 5.54 [835,] 5.50 [836,] 5.82 [837,] 5.72 [838,] 5.36 [839,] 5.54 [840,] 5.62 [841,] 5.28 [842,] 5.48 [843,] 5.50 [844,] 5.50 [845,] 5.60 [846,] 5.38 [847,] 5.36 [848,] 5.34 [849,] 5.36 [850,] 5.38 [851,] 5.66 [852,] 5.50 [853,] 5.34 [854,] 5.38 [855,] 5.60 [856,] 5.40 [857,] 5.24 [858,] 5.66 [859,] 5.74 [860,] 5.66 [861,] 5.48 [862,] 5.50 [863,] 5.46 [864,] 5.70 [865,] 5.66 [866,] 5.46 [867,] 5.42 [868,] 5.30 [869,] 5.50 [870,] 5.48 [871,] 5.36 [872,] 5.38 [873,] 5.48 [874,] 5.58 [875,] 5.42 [876,] 5.50 [877,] 5.54 [878,] 5.50 [879,] 5.54 [880,] 5.22 [881,] 5.28 [882,] 5.26 [883,] 5.32 [884,] 5.50 [885,] 5.48 [886,] 5.64 [887,] 5.40 [888,] 5.56 [889,] 5.36 [890,] 5.64 [891,] 5.64 [892,] 5.38 [893,] 5.32 [894,] 5.40 [895,] 5.36 [896,] 5.48 [897,] 5.34 [898,] 5.68 [899,] 5.50 [900,] 5.82 [901,] 5.74 [902,] 5.56 [903,] 5.52 [904,] 5.46 [905,] 5.54 [906,] 5.94 [907,] 5.78 [908,] 5.38 [909,] 5.78 [910,] 5.38 [911,] 5.30 [912,] 5.36 [913,] 5.62 [914,] 5.50 [915,] 5.54 [916,] 5.32 [917,] 5.26 [918,] 5.38 [919,] 5.36 [920,] 5.84 [921,] 5.42 [922,] 5.52 [923,] 5.50 [924,] 5.68 [925,] 5.30 [926,] 5.46 [927,] 5.48 [928,] 5.64 [929,] 5.46 [930,] 5.82 [931,] 5.30 [932,] 5.72 [933,] 5.82 [934,] 5.46 [935,] 5.32 [936,] 5.64 [937,] 5.44 [938,] 5.64 [939,] 5.40 [940,] 5.48 [941,] 5.48 [942,] 5.54 [943,] 5.54 [944,] 5.30 [945,] 5.66 [946,] 5.50 [947,] 5.48 [948,] 5.44 [949,] 5.46 [950,] 5.46 [951,] 5.68 [952,] 5.92 [953,] 5.46 [954,] 5.74 [955,] 5.40 [956,] 5.64 [957,] 5.42 [958,] 5.72 [959,] 5.56 [960,] 5.50 [961,] 5.34 [962,] 5.36 [963,] 5.70 [964,] 5.44 [965,] 5.52 [966,] 5.64 [967,] 5.42 [968,] 5.48 [969,] 5.72 [970,] 5.58 [971,] 5.30 [972,] 5.44 [973,] 5.36 [974,] 5.54 [975,] 5.66 [976,] 5.66 [977,] 5.32 [978,] 5.56 [979,] 5.62 [980,] 5.26 [981,] 5.48 [982,] 5.54 [983,] 5.38 [984,] 5.60 [985,] 5.68 [986,] 5.64 [987,] 5.48 [988,] 5.70 [989,] 5.92 [990,] 5.42 [991,] 5.34 [992,] 5.48 [993,] 5.72 [994,] 5.54 [995,] 5.34 [996,] 5.46 [997,] 5.84 [998,] 5.24 [999,] 5.46 [1000,] 5.80 ``` ] .pull-right[ **Original sample mean** ```r mean(height) ``` ``` [1] 5.5 ``` ] --- ## Make a histogram of the means of the 1000 bootstrap samples ```r df <- data.frame(mean=result$t) library(ggplot2) ggplot(df, aes(x=mean)) + geom_histogram(col="white")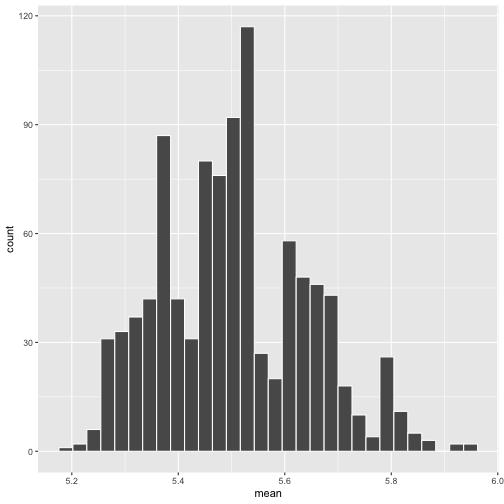 ``` <!-- --> --- ## Understanding the output ```r result ``` ``` ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = height, statistic = samplemean, R = 1000) Bootstrap Statistics : original bias std. error t1* 5.5 0.00528 0.1402647 ``` ```r mean(height) ``` ``` [1] 5.5 ``` ```r mean(result$t) - mean(height) ``` ``` [1] 0.00528 ``` ```r sd(result$t) ``` ``` [1] 0.1402647 ``` --- ## Confidence intervals via bootstrap (cont.) **Method 1:** The 95% bootstrap confidence interval is ```r c(sort(result$t)[25],sort(result$t)[975]) ``` ``` [1] 5.26 5.80 ``` **Method 2:** ```r boot.ci(result, type="all") ``` ``` Warning in boot.ci(result, type = "all"): bootstrap variances needed for studentized intervals ``` ``` BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 1000 bootstrap replicates CALL : boot.ci(boot.out = result, type = "all") Intervals : Level Normal Basic 95% ( 5.220, 5.770 ) ( 5.200, 5.739 ) Level Percentile BCa 95% ( 5.261, 5.800 ) ( 5.280, 5.820 ) Calculations and Intervals on Original Scale ``` --- ## Confidence intervals via bootstrap (cont.) 1. Normal 2. Basic 3. Percentile 4. BCa (“Bias Corrected and Accelerated) Reading here: https://www.r-bloggers.com/2019/09/understanding-bootstrap-confidence-interval-output-from-the-r-boot-package/ --- ## Hypothesis testing `$$H_0: \mu =5$$` `$$H_1: \mu \neq 5$$` ```r boot.ci(result, type="all") ``` ``` Warning in boot.ci(result, type = "all"): bootstrap variances needed for studentized intervals ``` ``` BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 1000 bootstrap replicates CALL : boot.ci(boot.out = result, type = "all") Intervals : Level Normal Basic 95% ( 5.220, 5.770 ) ( 5.200, 5.739 ) Level Percentile BCa 95% ( 5.261, 5.800 ) ( 5.280, 5.820 ) Calculations and Intervals on Original Scale ``` 5 is outside the interval. Hence, `\(H_0\)` would be rejected under 0.05 level of significance. We can conclude that population mean is significantly different from 5. --- ## Your turn Compute bootstrap confidence interval for median. data: `heights` --- ## Answer ```r samplemedian <- function(data, indices) { return(median(data[indices])) } resultmedian <- boot(data = height, statistic = samplemedian, R = 1000) resultmedian ``` ``` ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = height, statistic = samplemedian, R = 1000) Bootstrap Statistics : original bias std. error t1* 5.4 0.0348 0.1904343 ``` --- ## Answer (cont.) ```r boot.ci(resultmedian, type="all") ``` ``` Warning in boot.ci(resultmedian, type = "all"): bootstrap variances needed for studentized intervals ``` ``` BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 1000 bootstrap replicates CALL : boot.ci(boot.out = resultmedian, type = "all") Intervals : Level Normal Basic 95% ( 4.992, 5.738 ) ( 4.700, 5.600 ) Level Percentile BCa 95% ( 5.2, 6.1 ) ( 5.2, 5.5 ) Calculations and Intervals on Original Scale Some BCa intervals may be unstable ``` --- ## Jackknife Approach - Unlike bootstrap, jackknife is an iterative process. A parameter is calculated on the whole dataset and it is repeatedly recalculated by removing an element one after another. - The main application of jackknife is to reduce bias and evaluate variance for an estimator. --- ## Exercise Construct - CIs for median `Sepal.Length`, - CIs for median `Sepal.Width` and - CIs for Spearman's rank correlation coefficient between `Sepal.Length` and `Sepal.Width` using bootstrap sampling. Data: `iris` --- class: center, middle Slides available at: https://thiyanga.netlify.app/courses/rmsc2020/contentr/ All rights reserved by [Thiyanga S. Talagala](https://thiyanga.netlify.com/)